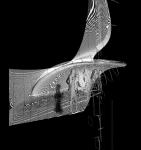
The art gallery allows views into and through it, collaging the existing city context by reflecting views from the galllery`s surfaces. The tower dislocates the viewer from their current environment acting as a filter to create an illusion, blurring the edges of the city and the tower.
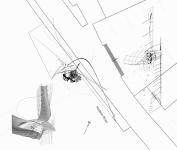
The Tower sits on the edge of a pier in Manhattan`s Battery Park. It screens, reflects and alters the urban fabric. The building programme consists of an ever-increasing gallery space that sits within the suspended surface, which envelops it. Its plans do not dictate the Tower`s perceived presence, because its pattern iterations are distorted by reflecting geometries (dislocating physical from perceived), which affect the manner in which the individual appropriates and engages with this space. Both fractal reflections and physical hyperbolic geometries simulate an illusion of the Tower project.
Dimensions describe the physical world, and parameters within those dimensions, such as light levels, alter our perceptions and in turn our relationship with these descriptions. This allows for an adaptation of Cartesian geometry and Gestalt psychology to address the non-Euclidean within our surroundings. With regard to the Tower, the imagined/subjectively perceived space is translated and continually morphed as a result of the surface renderings and reflections, whose boundaries and physical transitions are non-static, thus creating a dynamic series of dimensions. The reflecting surfaces have a Hausdorff dimension12 greater than its topological dimension, with the aim of presenting an infinite number of geometric iterations of an infinite length while the area remains finite.
The surface reflections, however, are too irregular to be easily described using a traditional Euclidean geometric language. Both these criteria are characteristics of fractal as a geometric object.
Julia fractal configuration, non-specific scale hyperbolic geometry distorts surface iterations
Fractals epitomised complex dimensions before the invention of computers. A fractal is neither one or two-dimensional; rather it is of a fractional dimension, because its complex geometry suggests its surface. No single, small piece of it is line-like, but neither does it describe a plane. It is too big to be thought of as a one-dimensional object, but too thin to be of two dimensions. It’s dimension is most accurately described by a number between one and two. Fractal dimensions reserve self-similarity across scales, only being restricted through context. Scale invariance is an exact form of self-similarity where at any magnification there is a smaller piece of the object that is similar to the whole. The reason I use this as a tool for the Tower`s design criteria is to separate the perception and appropriation of Euclidean geometry and space from the constraints of expectation and as an analogy to its vertical gallery and exhibition typology.
The Tower project therefore attempts to present a projected physicality, reiterating that the tangibility of architectural dimension is expanding along with our objective world. What can be imagined can be communicated using a lexicon of dimension.
2008
2009
.jpg)
.jpg)
.jpg)
.jpg)


.jpg)

